Feature-learning deep nets progressively collapse data to a regular low-dimensional geometry. How this emerges from the collective action of nonlinearity, noise, learning rate, and other factors, has eluded first-principles theories built from microscopic neuronal dynamics. We exhibit a noise–nonlinearity phase diagram that identifies regimes where shallow or deep layers learn more effectively and propose a macroscopic mechanical theory that reproduces the diagram and links feature learning across layers to generalization.
This work was featured by the University of Basel in a research highlight article.
Deep net and phenomenological model
Deep neural networks (DNNs) progressively compute features from which the final layer generates predictions. When optimized via stochastic dynamics over a data-dependent energy, each layer learns to compute better features than the previous one, ultimately transforming the data to a regular low-dimensional geometry. How it emerges from microscopic interactions between millions of artificial neurons is a central open question in deep learning.
In this work, we take a thermodynamical, top-down approach and look for a simple phenomenological model which captures the feature learning phenomenology. We show that DNNs can be mapped to a phase diagram defined by noise and nonlinearity, with phases where layers learn features uniformly, and where deep or shallow layers learn better. Better is quantified through data separation --- the ratio of feature variance within and across classes.
Phase diagram
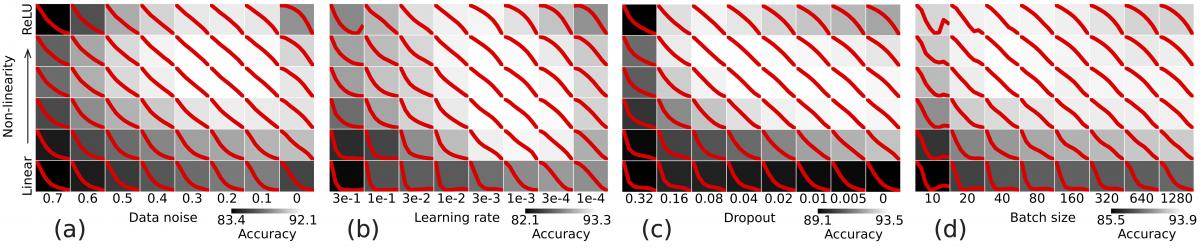
Figure: Phase diagrams of DNN training load curves (red) for nonlinearity vs. (a) data noise, (b) learning rate, (c) dropout, and (d) batch size.
In these phase diagrams, all panels the abscissas measure stochasticity and the ordinates nonlinearity. We control nonlinearity by varying the slope of the negative part of a LeakyReLU activation. Consider for example (a) where noise is introduced in labels and data (we randomly reset a fraction p of the labels, and add Gaussian noise with variance p2 to data). Without noise (upper right corner), the load curve is concave; this resembles an RFM or a kernel machine. Increasing noise (right to left) yields a linear and then a convex load curve.
The same phenomenology results from varying learning rate, dropout, and batch size (b, c, d). Lower learning rate, smaller dropout, and larger batch size all indicate less stochasticity in dynamics. Martin and Mahoney call them temperature-like parameters. In all cases high nonlinearity and low noise result in a concave load curve where parameters of deep layers move faster than those of shallow. Low nonlinearity and high noise (bottom-left) result in convex load curves. We observe the same behavior for other datasets (e.g., CIFAR10) and network architectures (e.g., CNNs).
Spring block model
To explain this phase diagram, we propose a macroscopic theory of feature learning in deep, nonlinear neural networks: we show that the stochastic dynamics of a nonlinear spring--block chain with asymmetric friction fully reproduce the phenomenology of data separation over training epochs and layers. The phase diagram is universal with respect to the source of stochasticity: varying dropout rate, batch size, label noise, or learning rate all result in the same phenomenology.
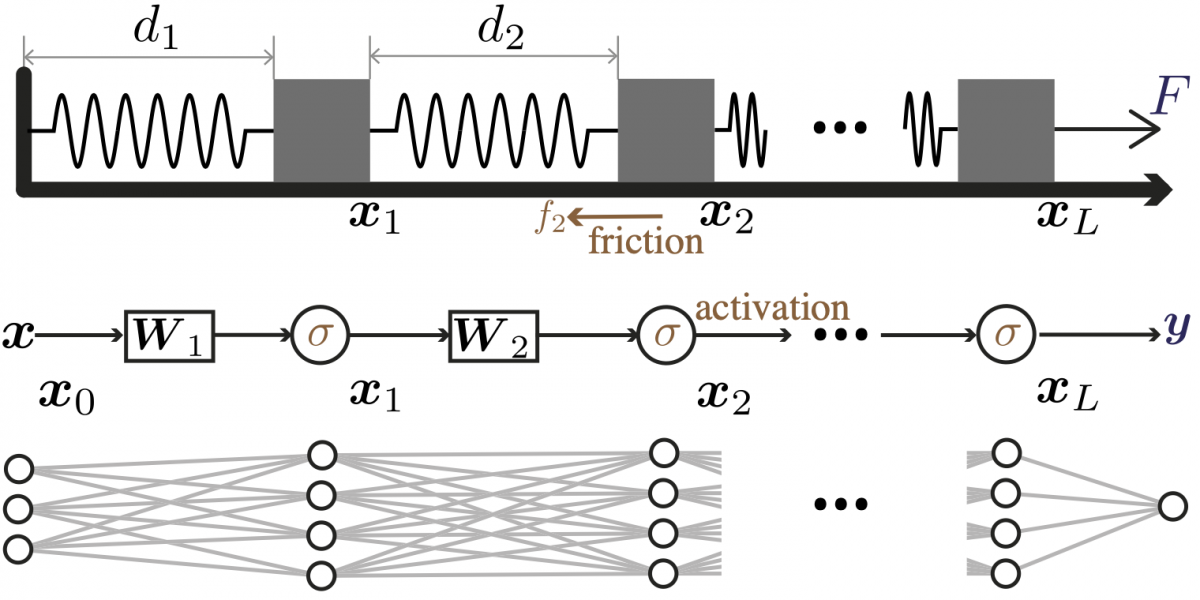
Figure: An illustration of the analogy between a spring–block
chain and a deep neural network.
The spring-block model exhibits similarities not only in the phase diagrams but also in the entire training dynamics, as shown in the following figure. Specifically, a1, c1, b1, and d2 represent the trajectories from training a deep neural network, while a2, b2, c2, and d2 correspond to the trajectories of the spring-block model.
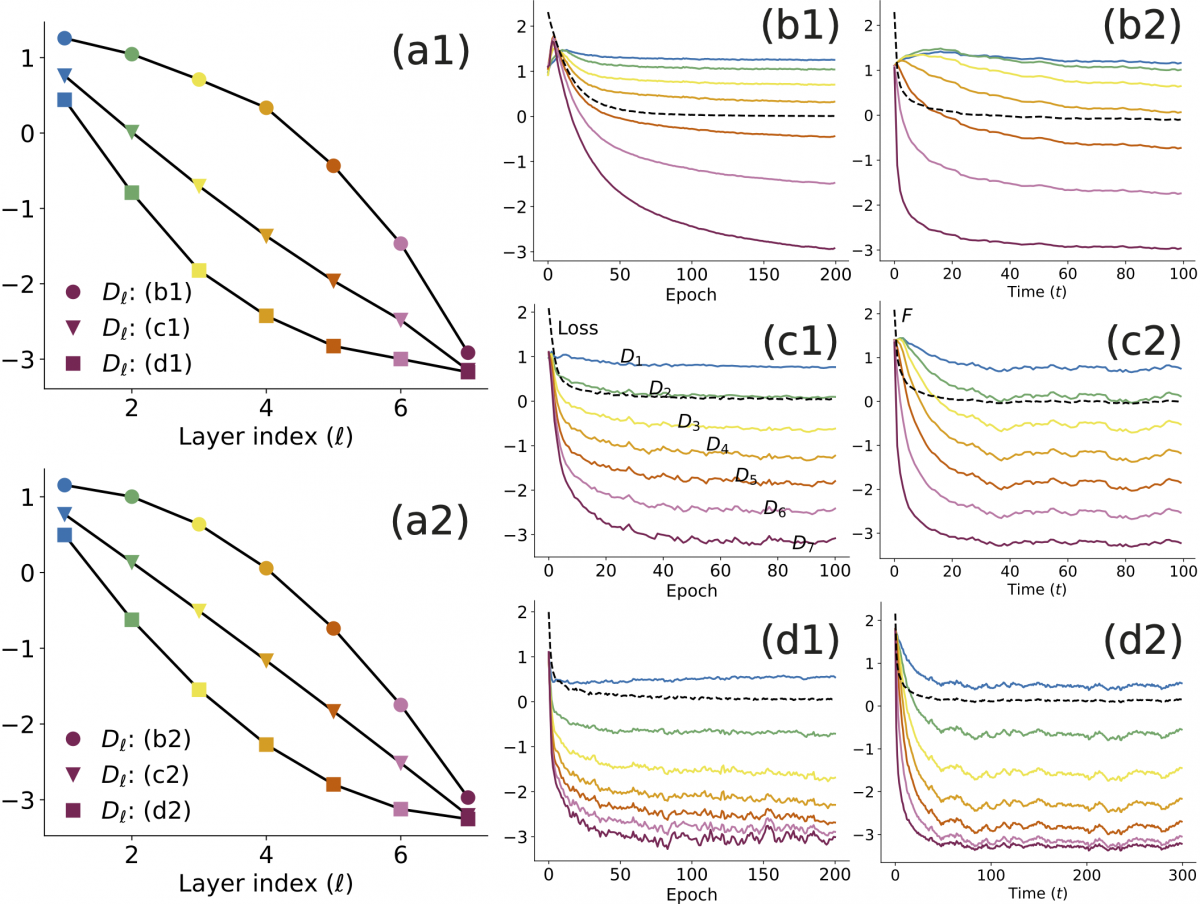
Figure: The load curves at convergence (a) and trajectories (b, c, d) for a 7−hidden layer ReLU MLP on MNIST ( _1) vs our spring–block model ( _2).
Toy experiment
We also demonstrate a common cascaded mechanical system--a folding ruler--exhibits a phenomenology which is in some ways reminiscent of feature learning dynamics in DNNs.

Figure: Pulling an in-folding ruler illustrates load distribution.
In this experiment we pin the left end of the in-folding ruler and pull the right end by hand. Due to friction, if we pull it very slowly and steadily, the outer layer extends far while the inner layers are close to stuck. This reminds us of lazy training where the outer layers take the largest proportion of the load. Conversely, shaking while pulling helps activate the inner layers and redistribute the force, and ultimately results in a uniformly distributed extension of each layer. Videos can be found at https://github.com/DaDaCheng/DNN_Spring.
Publications
2025
@article{ys4n-2tj3,
title = {Spring-block theory of feature learning in deep neural networks},
author = {Shi, Cheng and Pan, Liming and Dokmanić, Ivan},
journal = {Phys. Rev. Lett.},
pages = {--},
year = {2025},
month = {May},
publisher = {American Physical Society},
doi = {10.1103/ys4n-2tj3},
url = {https://link.aps.org/doi/10.1103/ys4n-2tj3}
}