Implicit neural representation is a promising new paradigm that leverages deep learning to approximate the continuous representation of a signal. This approach characterizes the continuous representation using a deep neural network that takes feature coordinates as input and returns features. By using continuous parametrization, implicit neural representations offer significant advantages over traditional methods like discrete grid-based representations. Specifically, they are more memory-efficient and enable the computation of spatial derivatives, which is crucial for solving partial differential equations (PDEs). Our ongoing projects are focused on exploring the potential of implicit neural representations in solving imaging inverse problems.
FunkNN: Neural Interpolation for Functional Generation
Can we build continuous generative models which generalize across scales, can be evaluated at any coordinate, admit calculation of exact derivatives, and are conceptually simple? Existing MLP-based architectures generate worse samples than the grid-based generators with favorable convolutional inductive biases. Models that focus on generating images at different scales do better, but employ complex architectures not designed for continuous evaluation of images and derivatives. We take a signal-processing perspective and treat continuous image generation as interpolation from samples. Indeed, correctly sampled discrete images contain all information about the low spatial frequencies. The question is then how to extrapolate the spectrum in a data-driven way while meeting the above design criteria. Our answer is FunkNN---a new convolutional network which learns how to reconstruct continuous images at arbitrary coordinates and can be applied to any image dataset. Combined with a discrete generative model it becomes a functional generator which can act as a prior in continuous ill-posed inverse problems. We show that FunkNN generates high-quality continuous images and exhibits strong out-of-distribution performance thanks to its patch-based design. We further showcase its performance in several stylized inverse problems with exact spatial derivatives.
Github: https://github.com/swing-research/FunkNN
Arxiv: https://arxiv.org/abs/2212.14042
OpenReview: https://openreview.net/forum?id=BT4N_v7CLrk
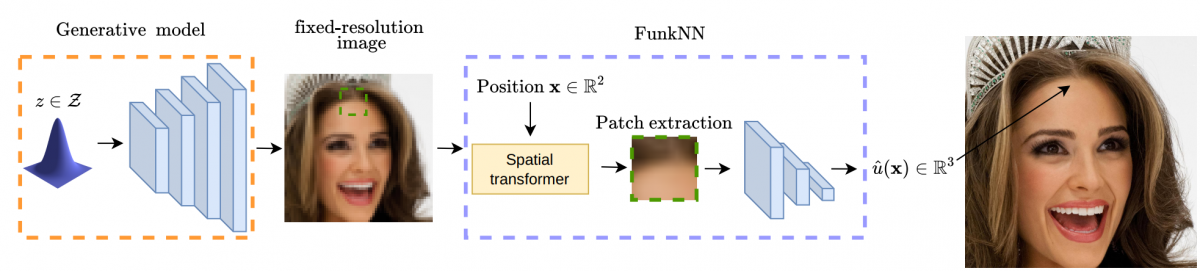
Figure: The proposed architecture. The generative model (orange) produces a fixed-resolution image that is differentiably used by FunkNN to produce the image intensity at any location (blue).
Implicit Neural Representation for Mesh-Free Inverse Obstacle Scattering
Implicit representation of shapes as level sets of multilayer perceptrons has recently flourished in different shape analysis, compression, and reconstruction tasks. In this paper, we introduce an implicit neural representation-based framework for solving the inverse obstacle scattering problem in a mesh-free fashion. We express the obstacle shape as the zero-level set of a signed distance function which is implicitly determined by network parameters. To solve the direct scattering problem, we implement the implicit boundary integral method. It uses projections of the grid points in the tubular neighborhood onto the boundary to compute the PDE solution directly in the level-set framework. The proposed implicit representation conveniently handles the shape perturbation in the optimization process. To update the shape, we use PyTorch's automatic differentiation to backpropagate the loss function w.r.t. the network parameters, allowing us to avoid complex and error-prone manual derivation of the shape derivative. Additionally, we propose a deep generative model of implicit neural shape representations that can fit into the framework. The deep generative model effectively regularizes the inverse obstacle scattering problem, making it more tractable and robust, while yielding high-quality reconstruction results even in noise-corrupted setups.
Arxiv: https://arxiv.org/abs/2206.02027
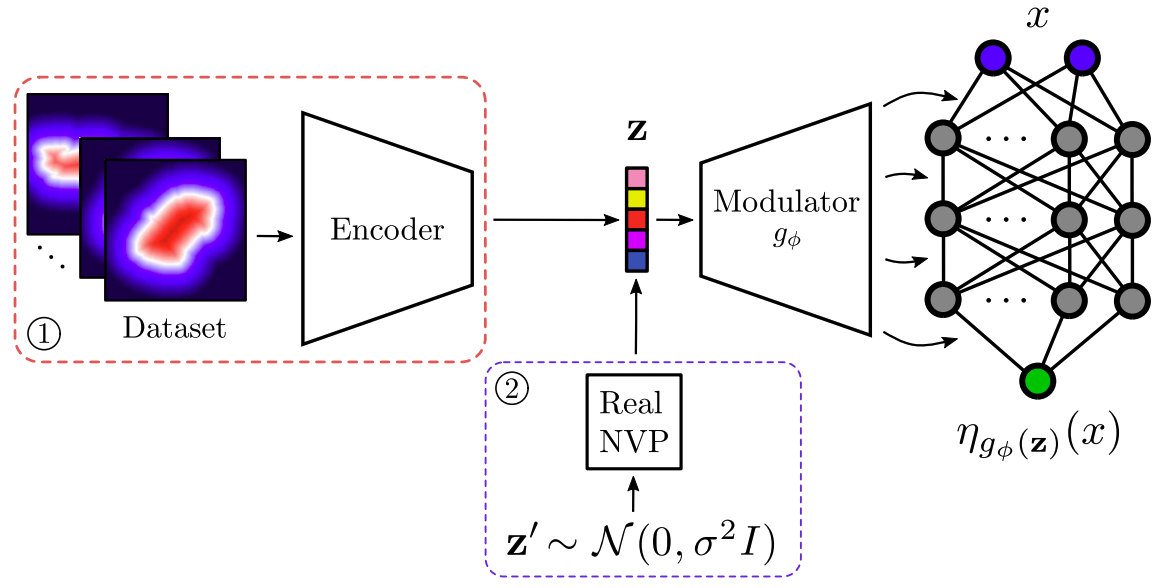
Figure: Generative modeling of implicit neural representations.
Differentiable Uncalibrated Imaging
We propose a differentiable imaging framework to address uncertainty in measurement coordinates such as sensor locations and projection angles. We formulate the problem as measurement interpolation at unknown nodes supervised through the forward operator. To solve it we apply implicit neural networks, also known as neural fields, which are naturally differentiable with respect to the input coordinates. We also develop differentiable spline interpolators which perform as well as neural networks, require less time to optimize and have well-understood properties. Differentiability is key as it allows us to jointly fit a measurement representation, optimize over the uncertain measurement coordinates, and perform image reconstruction which in turn ensures consistent calibration. We apply our approach to 2D and 3D computed tomography and show that it produces improved reconstructions compared to baselines that do not account for the lack of calibration. The flexibility of the proposed framework makes it easy to apply to almost arbitrary imaging problems.
Arxiv: https://arxiv.org/abs/2211.10525
Figure: Visualization of the parameter mismatch.
Joint Cryo-ET Alignment and Reconstruction with Neural Deformation Fields
We propose a framework to jointly determine the deformation parameters and reconstruct the unknown volume in electron cryotomography (CryoET). CryoET aims to reconstruct three-dimensional biological samples from two-dimensional projections. A major challenge is that we can only acquire projections for a limited range of tilts, and that each projection undergoes an unknown deformation during acquisition. Not accounting for these deformations results in poor reconstruction. The existing CryoET software packages attempt to align the projections, often in a workflow which uses manual feedback. Our proposed method sidesteps this inconvenience by automatically computing a set of undeformed projections while simultaneously reconstructing the unknown volume. We achieve this by learning a continuous representation of the undeformed measurements and deformation parameters. We show that our approach enables the recovery of high-frequency details that are destroyed without accounting for deformations.
Arxiv: https://arxiv.org/abs/2211.14534
Publications
2023
@article{khorashadizadeh2022funknn,
title={FunkNN: Neural Interpolation for Functional Generation},
author={Khorashadizadeh, AmirEhsan and Chaman, Anadi and Debarnot, Valentin and Dokmani{\'c}, Ivan},
journal={ICLR},
year={2023},
projectpage = {https://sada.dmi.unibas.ch/en/research/implicit-neural-representation},
volume={abs/2212.14042},
eprint={2212.14042},
archivePrefix={arXiv},
url={https://openreview.net/forum?id=BT4N_v7CLrk}
}2022
@article{vlavsic2022implicit,
title={Implicit Neural Representation for Mesh-Free Inverse Obstacle Scattering},
author={Vla{\v{s}}i{\'c}, Tin and Nguyen, Hieu and Khorashadizadeh, AmirEhsan and Dokmani{\'c}, Ivan},
journal={56th Asilomar Conference on Signals, Systems, and Computers},
year={2022},
projectpage = {http://sada.dmi.unibas.ch/en/research/injective-flows},
volume={abs/2206.02027},
eprint={2206.02027},
archivePrefix={arXiv}
}