Wave propagation plays a key role in almost all imaging modalities---from seismic tomography used for earthquake localization to medical photoacoustic tomography used for fast high-resolution scanning of human tissues.
Below we show an example simulation of the Virgina Earthquake [Courtesy: Oxford Seismology] propagating from its epicenter. One can see the complex morphing of the inital spherical wavefront as the wave propagates. As the wavefront propagates it is captured by stations located across the planet. We can then use the information from multiple stations to localize earthquakes. Using conventional signal processing techniques we are currently unable to localize small magnitude earthquakes. However, there are exponentially more small magnitude earthquakes compared to the larger ones. Therefore, if we localize them, we will have a much larger library of earthquakes to study to understand the geology of our planet and others. Can we leverage machine learning for the same?

Another application is photoacoustic tomography (PAT) --- an exciting medical imaging modality that enables fast high-resolution imaging without using any ionizing radiation. This is now being developed for breast cancer screening applications. The images seen below are examples of reconstructed images from PAT imaging.
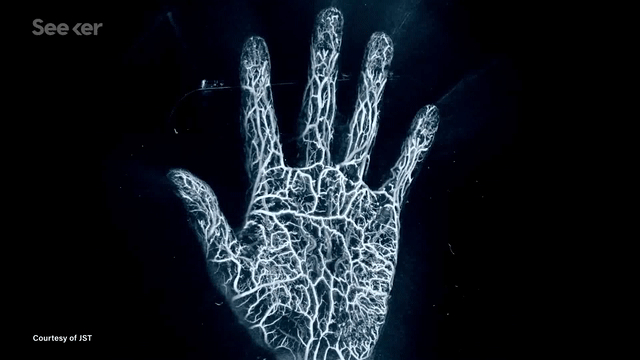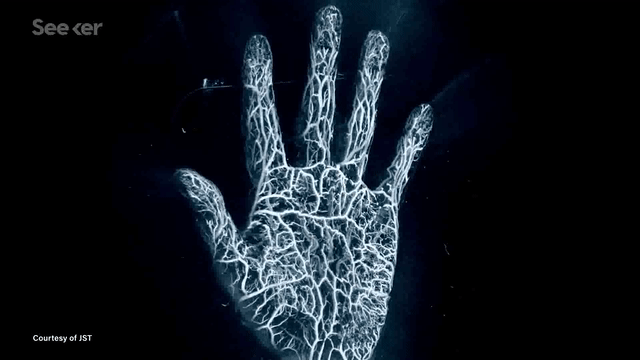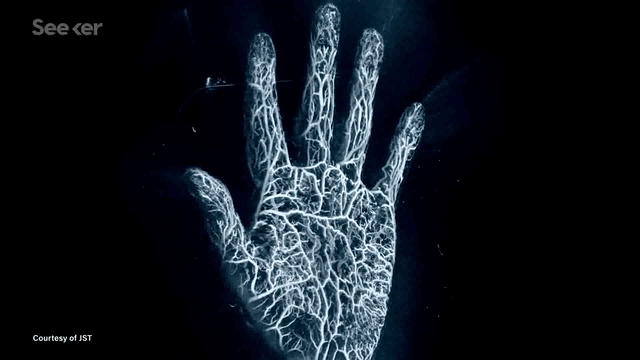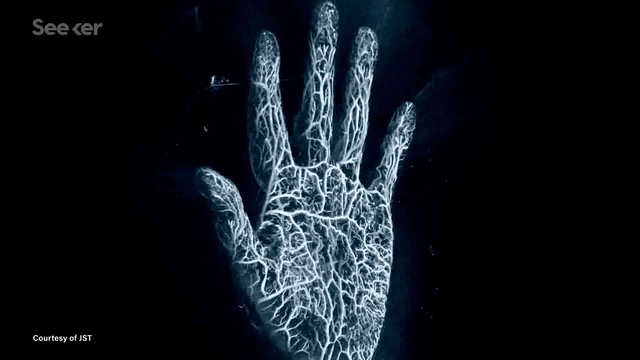
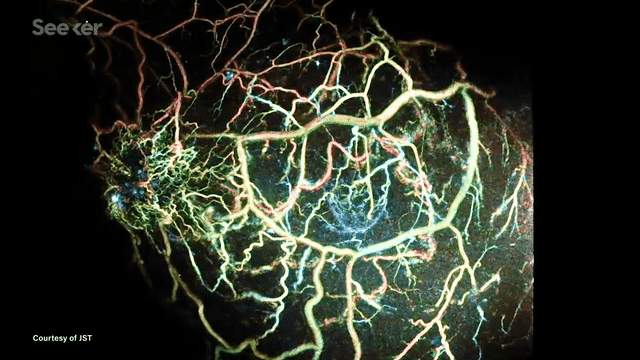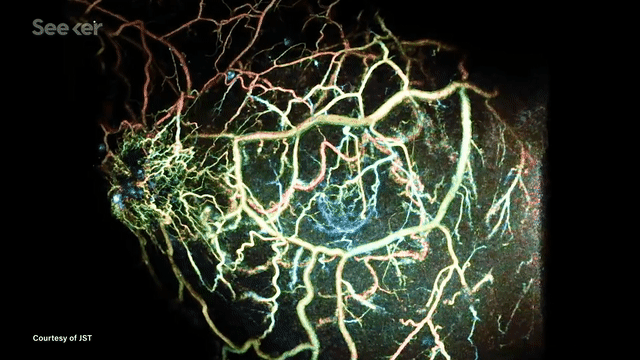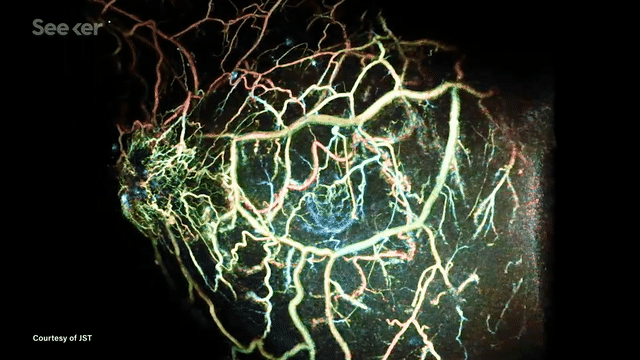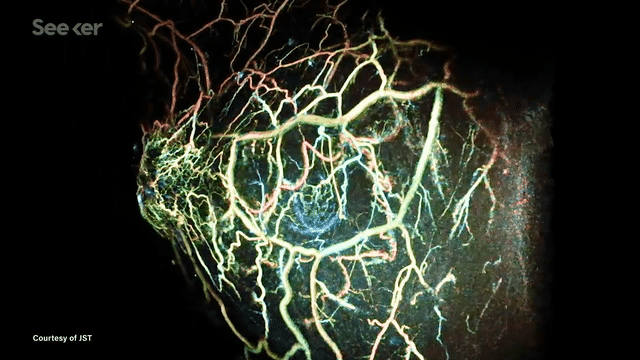
In many such imaging modalities we have very little ground truth data. This is either due to data collection being expensive (for example doing PAT scans of many patients) or infeasible (for example when exploring other planets). The common theme in these and many other imaging modalities is that they follow the wave equation.
We ask how can we leverage this physics in our learning-based solutions? How can we train these models without having access to ground-truth data? If we do not have the ground-truth how do we build confidence in our models?
Fourier integral operators
Our proposed method is based on Fourier integral operators (FIO) which are solution operators of the wave equation for high frequency waves. An FIO is written as
\[ [F_\sigma u](y) = \int_\xi a(y,\xi) u(\xi) \exp(iS_\sigma (y,\xi)d\xi \]
Here \( u \) is the object being imaged---this could be the tissues, or the subsurface of the earth, or even atomic crystals in microscopy, \( \xi \) corresponds to the conjugate spatial frequency variable, \(a(y,\xi)\) is the spatially varying convolution kernel, \( \sigma \) corresponds to the material parameter that controls the wave speed within the material and \(S(y,\xi)\) is called the phase of the FIO, \(F\). Many imaging modalities are studied under microlocal analysis using FIOs in order to mathematically characterize the artifacts that should be expected from the imaging modality, what regions of the object will be invisible to the imaging modality etc.
We follow the representation and discretization of FIOs in tight frames to come up with a neural architecture that learns wave motion in a physically interpretable fashion. To build the interpretability, it helps to think of waves as being composed of smaller elements called wave packets. These are oscillatory signals localized in both space and spatial frequency domains --- i.e. they have a location and orientation in space. At the scale of these wave packets the solution of the wave equation is coarsely approximated by solving a Hamiltonian system. This is very much like ray-tracing in geometrical optics. We explicitly force our networks to learn these solutions within our proposed FIONets. Please refer to the video below for a short description of the paper.
NeurIPS 2020 Spotlight talk
Current and future work
Lens and boundary rigidity problems
Say we have a convex, singly-connected body, \( B \subset \mathbb{R}^3 \) with a boundary \(\partial B\) and we are given travel times \(t_i \) between two points \(p_i\) and \(q_i\), where \(p_i, q_i \in \partial B\) for \(i \in [N]\). Our task is to recover the background wavespeed within \(B\). We assume that we also know the corresponding orientations of the wave front at \(p_i\) and \(q_i\). This is essential for making the problem well-posed. In absence of the orientation information, one would need data-specific priors for wave speed inversion.
Photoacoustic imaging for breast cancer screening
We want to use FIONet for reconstructing PAT images by training on arbitrary datasets.
Earthquake localization
We want to use the wavepacket routing network component of the FIONet for earthquake localization of small quakes.
Publications
2020
@inproceedings{kothari2020fionet,
author = {Kothari, Konik and de Hoop, Maarten and Dokmani{\'c}, Ivan},
booktitle = {Advances in Neural Information Processing Systems},
title = {Learning the Geometry of Wave-Based Imaging},
projectpage = {http://sada.dmi.unibas.ch/en/research/imaging-with-waves},
url = {https://proceedings.neurips.cc/paper/2020/file/5e98d23afe19a774d1b2dcbefd5103eb-Paper.pdf},
volume = {33},
year = {2020}
}