Joint Denoising and Rewiring (JDR)

When learning from graph data, the graph and the node features both give noisy information about the node labels. In this paper we propose an algorithm to jointly denoise the features and rewire the graph (JDR), which improves the performance of downstream node classification graph neural nets (GNNs). JDR works by aligning the leading spectral spaces of graph and feature matrices. It approximately solves the associated non-convex optimization problem in a way that handles graphs with multiple classes and different levels of homophily or heterophily. We theoretically justify JDR in a stylized setting and show that it consistently outperforms existing rewiring methods on a wide range of synthetic and real-world node classification tasks.

Imagine that you have a catalogue of paper citations. You also have a mathematical representation of the words in abstract of the papers. For a small fraction of the papers you know their category, e.g. computer science, physics or medicine. Your goal is to predict the category (class) of the remaining papers. The problem you are facing is called a transductive node classification problem.

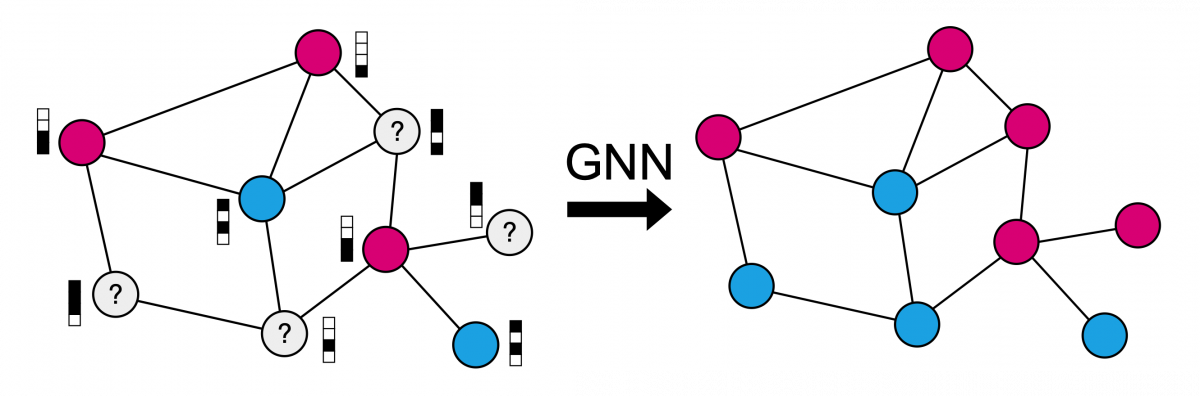
Figure 1: Visualization of the transductive node classification task. Papers are nodes and citations are edges in the graph. Paper features are indicated by the four-dimensional binary vectors and paper categories are indicated by the different color. The goal is to infer the color of the unknown papers. One algorithm to takle this problem is graph neural networks (GNNs).

Now the challenge is that some of the citations might be missing because the authors didn’t know about them and some might be added even though they are unnecessary, i.e. the graph structure is noisy and contains missing and spurious links. Also the features will be noisy, because the abstract always contains unnecessary words and can never describe the paper perfectly. This is where our method comes in.

The JDR algorithm

Joint denoising and rewiring (JDR) is an algorithm that preprocesses a graph dataset by jointly rewiring the graph and denoising the features to improve the performance of downstream node classification GNNs. 

Figure 2: Schematic overview of the JDR method.

We consider a noisy graph as it occurs in many different real-world scenarios, in the sense that it contains edges between and within classes and its node features are not fully aligned with the labels. The graph's adjacency matrix A and binary node features X are decomposed via spectral decomposition and singular value decomposition. The rewiring of A is performed by spectral interpolation between its own eigenvectors and the singular vectors in X. The same applies vice versa for denoising, and both are performed iteratively K times. We resynthesize the rewired and denoised graph by multiplying back the resulting matrices. To get specific properties like sparsity or binarity we can perform an Update step, e.g. by thresholding (as done above). 

Figure 3: Visualization of spectral interpolation step, for each of the leading vectors in A, we look for the most similar one in X and interpolate between the two.

To theoretically study our method we analyze graphs from a random generative graph community model, namely the contextualized stochastic block model (cSBM) (Deshpande et al., 2018). In this model, graphs are generated from a stochastic block model (SBM) and contextualized by Gaussian mixture model (GMM) features. 

Figure 4: Varying the graph signal strength parameter, the cSBM can create instances of graphs behaving in a random, homophilic or heterophilic way. The latter cases refer to the setting where nodes from the same class are more likely to connect than others (homophilic) and nodes from different classes are more likely to connect (heterophilic). 

Based on the above cSBM model and insights from random matrix theory, we proof that one iteration of JDR improves alignment of the leading eigen/singular vectors of the adjacency A and the features X with each other and the labels. We can also show this empirically in an actual experiment using graphs from the cSBM.

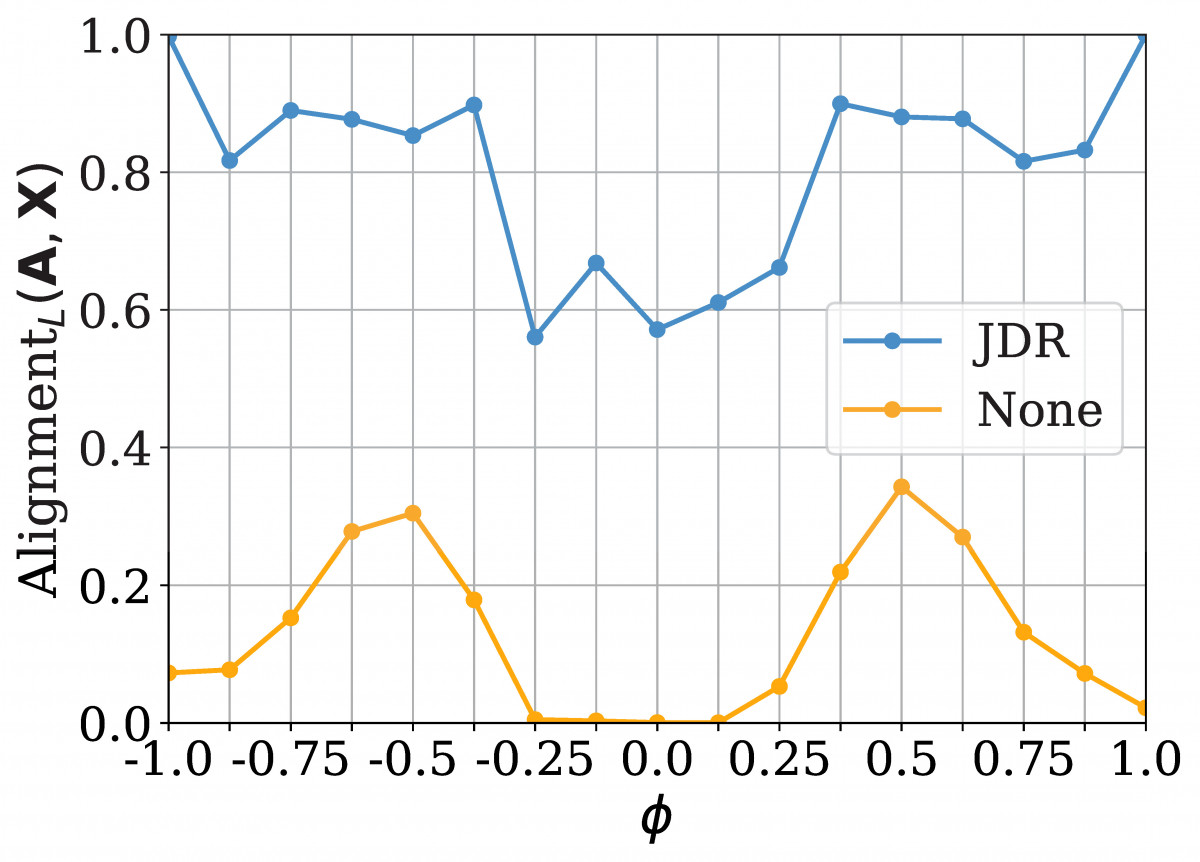
Figure 5: JDR clearly improves alignment across different graphs from the cSBM compared to the same graph without any processing.

We test JDR with two downstream GNNs, namely graph convolutional nets (GCN) and generalized page rank GNNs (GPRGNN) on different node classification tasks. On the synthetic data generated from the cSBM, we additionally compare to an MLP trained using only the node features and approximate message passing-belief propagation (AMP-BP), an optimal algorithm relying on knowing the distribution of the cSBM. It is thus not applicable to real-world graphs. 

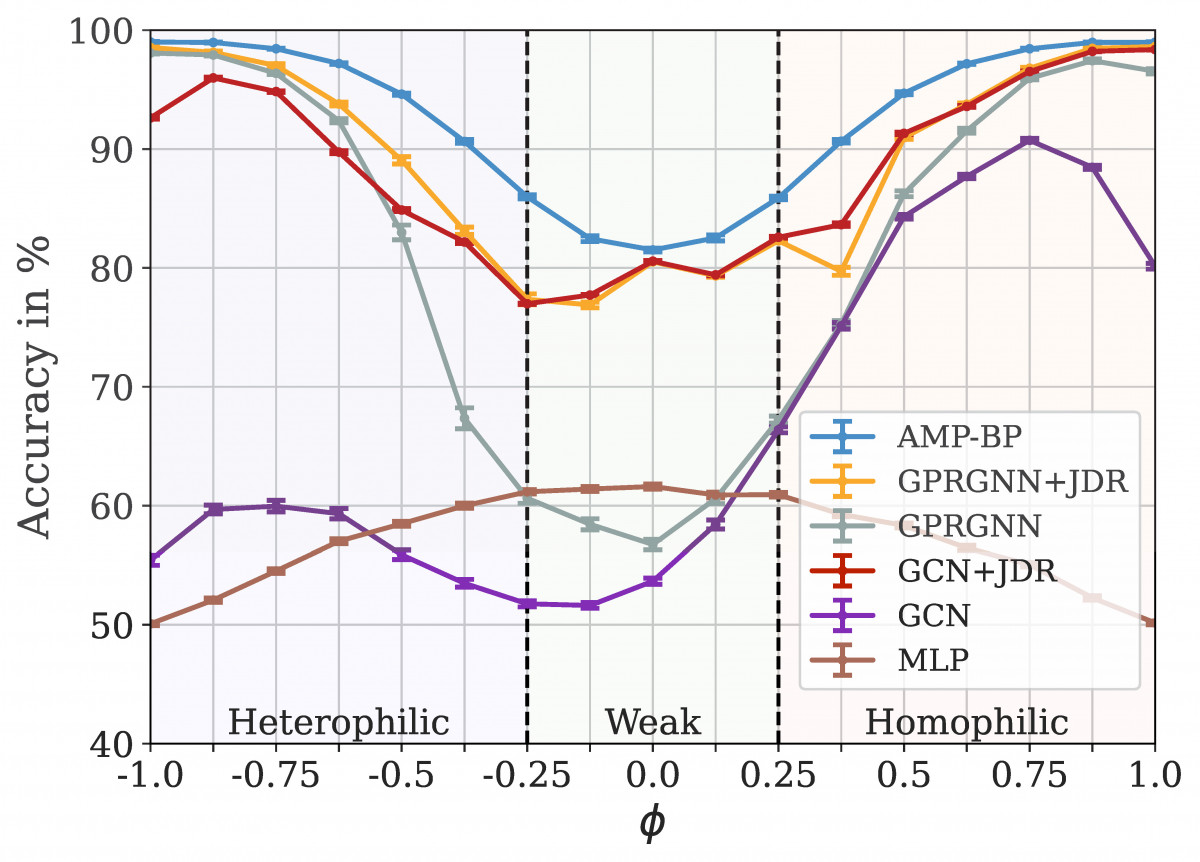
Figure 6: Test accuracy on graphs from the cSBM across different . For strongly homophilic and heterophilic graphs the features are close to random and in the weak graph regims the features contain most of the information. The error bars indicate the 95% confidence interval. JDR improves the performance for both GNNs across all graphs. 

We also test JDR on a variety of real world datasets, using different downstream algorithms, different splits and three state-of-the-art rewiring baselines, i.e. diffusion improves graph learning (DIGL) (Gasteiger et al., 2019), first-order spectral rewiring (FoSR) (Karhadkar et al., 2023) and batch Ollivier-Ricci flow (BORF) (Nguyen et al., 2023). JDR always significantly improves the performance in most of the scenarios most of the times beating the rewiring baselines. More experiments can be found in the paper and appendix.

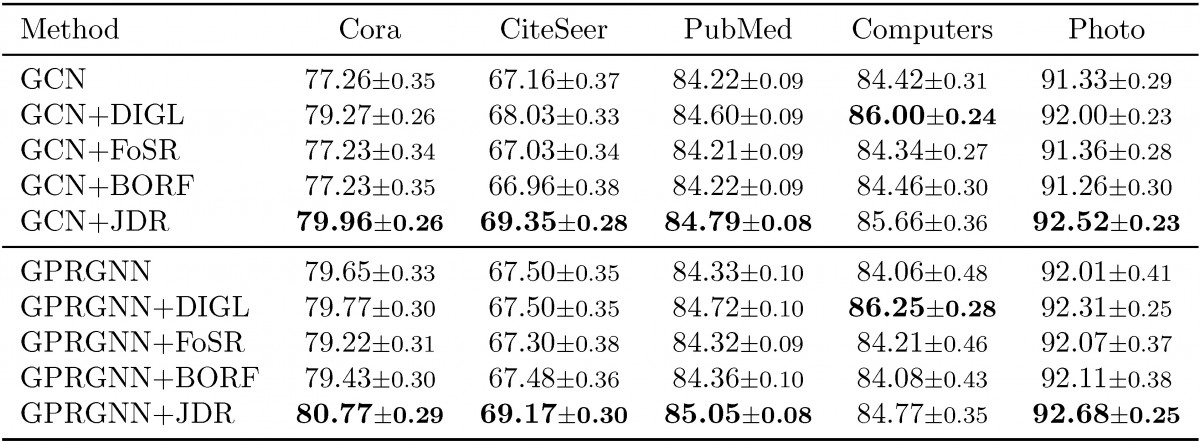
Table 1: Results on real-world homophilic datasets in the sparse splitting (2.5%/2.5%/95%): Mean accuracy across runs (%) +/- 95% confidence interval. Best average accuracy in bold.

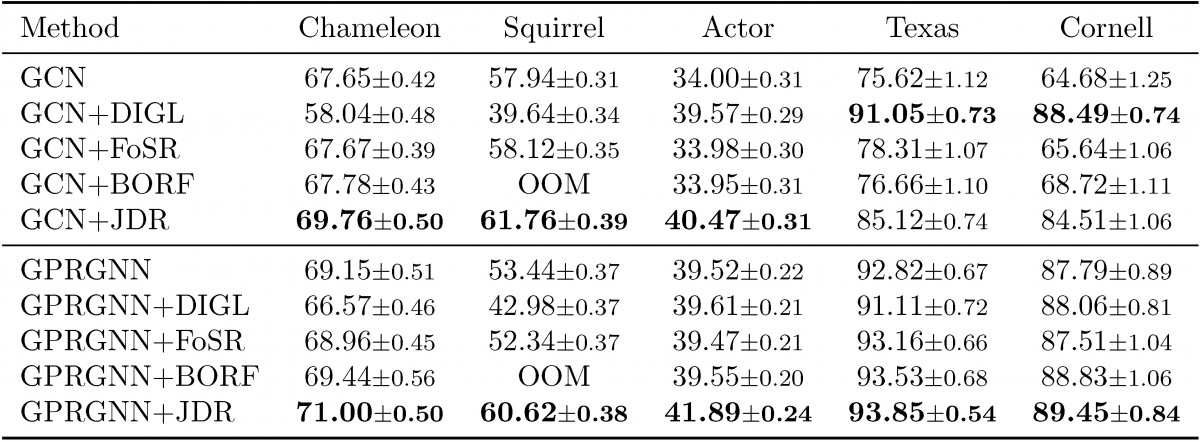
Table 2: Results on real-world heterophilic datasets in the dense splitting (60%/20%/20%): Mean accuracy across runs (%) +/- 95% confidence interval. Best average accuracy in bold.

To rerun JDR or adapt it to another dataset or GNN, download the files and install the necessary libraries. The installation and running instructions are provided in the repo: github.com/jlinki/JDR.