Generative models have shown great success in solving inverse problems. They can be used as a prior to regularizing the solution of an ill-posed problem, however, the choice of generative model is paramount. While Generative Adversarial Networks (GANs) can generate samples with impressive quality, they are shown to be unstable when used as a prior for solving inverse problems. Normalizing Flows alleviate some drawbacks of GANs by designing an invertible neural network apt for density estimation. However, they have their own drawbacks; having the same dimension in the latent and data spaces leads to a large network and poor performance for solving ill-posed inverse problems. In this series of projects, we design new families of generative models well-suited for solving ill-posed inverse problems.
Globally Injective ReLU Networks
In [Puthawala et al, 2020], we establish sharp characterizations of injectivity of fully-connected and convolutional ReLU layers and ReLU networks. First, through a layerwise analysis, we show that an expansivity factor of two is necessary and sufficient for injectivity by constructing appropriate weight matrices. We show that global injectivity with iid Gaussian matrices, a commonly used tractable model, requires larger expansivity between 3.4 and 10.1. We also characterize the stability of inverting an injective network via worst-case Lipschitz constants of the inverse. We then use arguments from differential topology to study injectivity of deep networks and prove that any Lipschitz map can be approximated by an injective ReLU network. Finally, using an argument based on random projections, we show that an end-to-end---rather than layerwise---doubling of the dimension suffices for injectivity. Our results establish a theoretical basis for the study of nonlinear inverse and inference problems using neural networks.
Arxiv: https://arxiv.org/abs/2006.08464
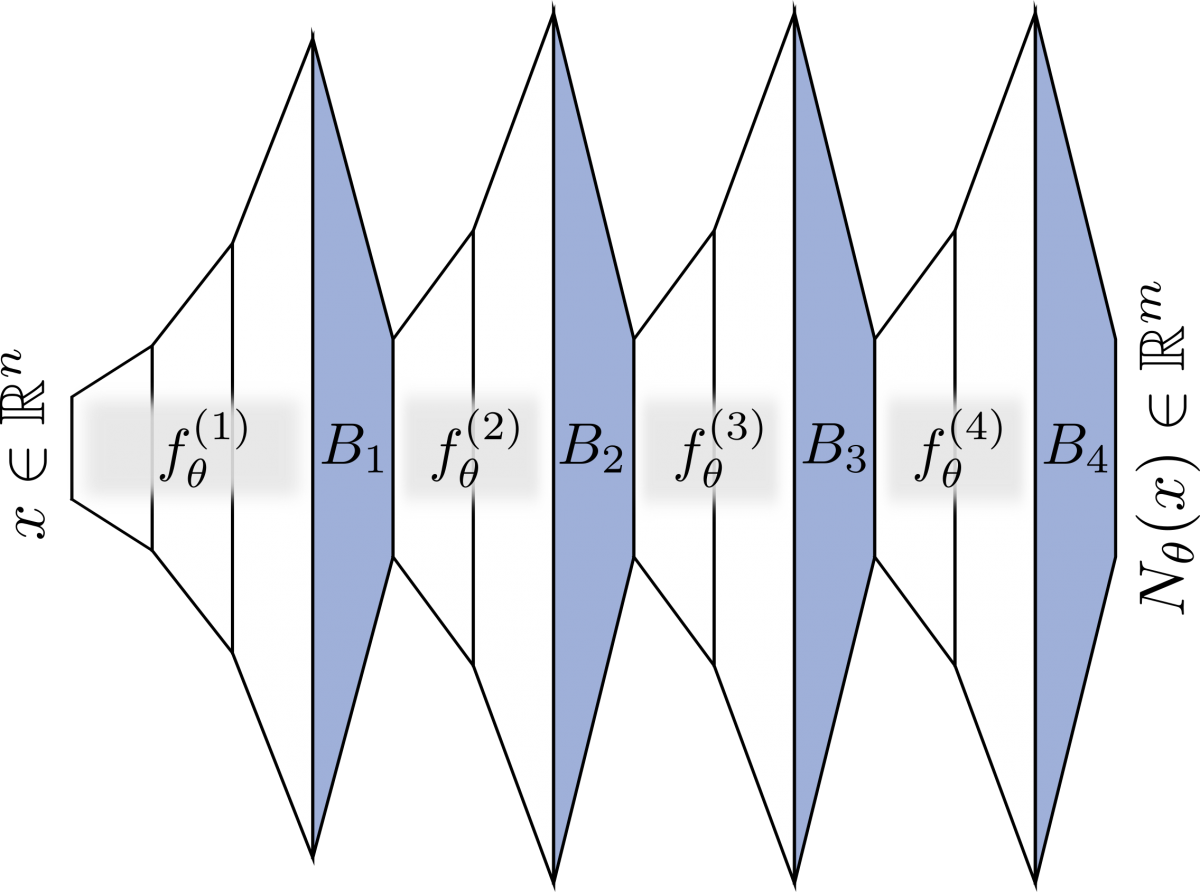
Figure: An illustration of an injective deep neural network that avoids expansivity. White trapezoids are expansive weight matrices and the blue trapezoids are random projectors that reduce dimension while preserving injectivity.
Trumpets: Injective Flows for Inference and Inverse Problems
Building on our results from Puthawala et al, 2020, we propose injective generative models called TRUMPETs that generalize invertible normalizing flows. The proposed generators progressively increase dimension from a low-dimensional latent space. We demonstrate that TRUMPETs can be trained orders of magnitudes faster than standard flows while yielding samples of comparable or better quality. They retain many of the advantages of the standard flows such as training based on maximum likelihood and a fast, exact inverse of the generator. Since TRUMPETs are injective and have fast inverses, they can be effectively used for downstream Bayesian inference. To wit, we use TRUMPET priors for maximum a posteriori estimation in the context of image reconstruction from compressive measurements, outperforming competitive baselines in terms of reconstruction quality and speed. We then propose an efficient method for posterior characterization and uncertainty quantification with TRUMPETs by taking advantage of the low-dimensional latent space.
GitHub: https://github.com/swing-research/trumpets
Arxiv: https://arxiv.org/abs/2102.10461
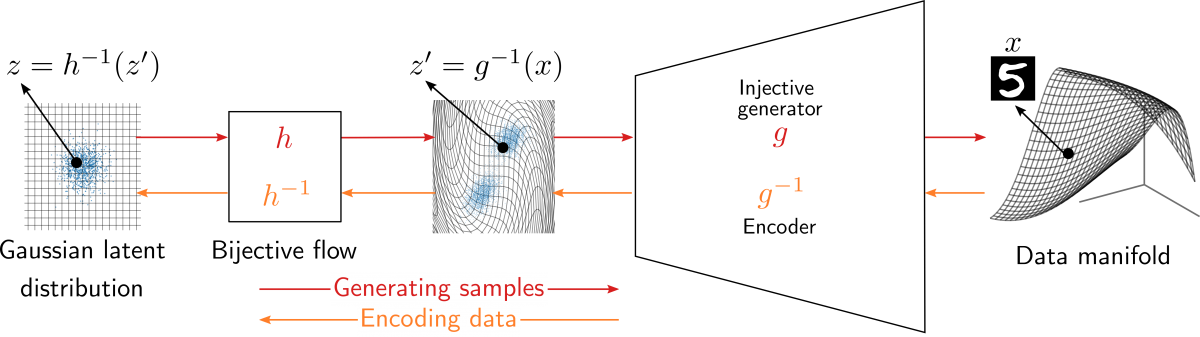
Figure: TRUMPET — A reversible injective flow-based generator.
Conditional Injective Flows for Bayesian Imaging
Most deep learning models for computational imaging regress a single reconstructed image. In practice, however, ill-posedness, nonlinearity, model mismatch, and noise often conspire to make such point estimates misleading or insufficient. The Bayesian approach models images and (noisy) measurements as jointly distributed random vectors and aims to approximate the posterior distribution of unknowns. Recent variational inference methods based on conditional normalizing flows are a promising alternative to traditional MCMC methods, but they come with drawbacks: excessive memory and compute demands for moderate to high resolution images and underwhelming performance on hard nonlinear problems. In this work, we propose C-Trumpets---conditional injective flows specifically designed for imaging problems, which greatly diminish these challenges. Injectivity reduces memory footprint and training time while low-dimensional latent space together with architectural innovations like fixed-volume-change layers and skip-connection revnet layers, C-Trumpets outperform regular conditional flow models on a variety of imaging and image restoration tasks, including limited-view CT and nonlinear inverse scattering, with a lower compute and memory budget. C-Trumpets enable fast approximation of point estimates like MMSE or MAP as well as physically-meaningful uncertainty quantification.
GitHub: https://github.com/swing-research/conditional-trumpets
Arxiv: https://arxiv.org/abs/2204.07664
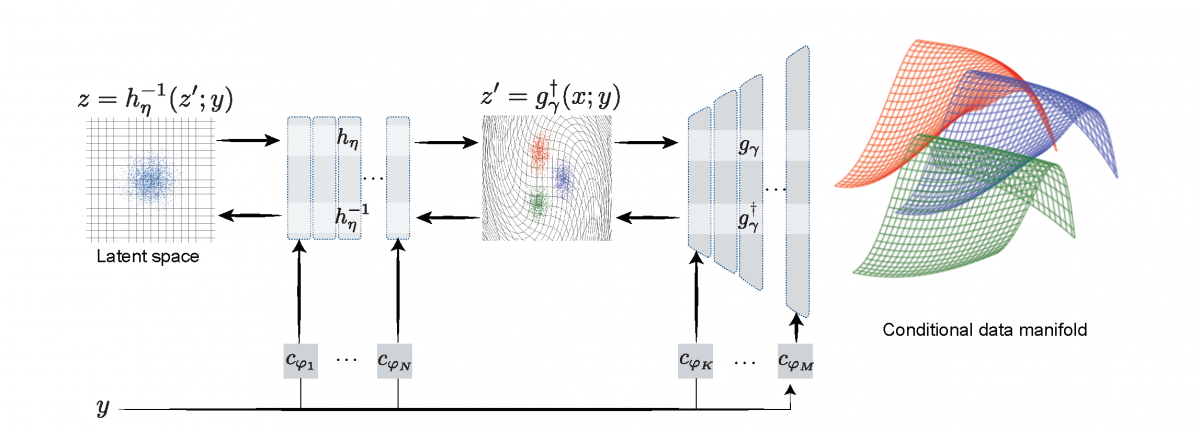
Figure: Conditional injective flows. Different measurements y1, y2 and y3 give different manifolds.
Deep Variational Inverse Scattering
Inverse medium scattering solvers generally reconstruct a single solution without an associated measure of uncertainty. This is true both for the classical iterative solvers and for the emerging deep learning methods. But ill-posedness and noise can make this single estimate inaccurate or misleading. While deep networks such as conditional normalizing flows can be used to sample posteriors in inverse problems, they often yield low-quality samples and uncertainty estimates. In this paper, we propose U-Flow, a Bayesian U-Net based on conditional normalizing flows, which generates high-quality posterior samples and estimates physically-meaningful uncertainty. We show that the proposed model significantly outperforms the recent normalizing flows in terms of posterior sample quality while having comparable performance with the U-Net in point estimation.
GitHub: https://github.com/swing-research/U-Flow
Arxiv: https://arxiv.org/abs/2212.04309
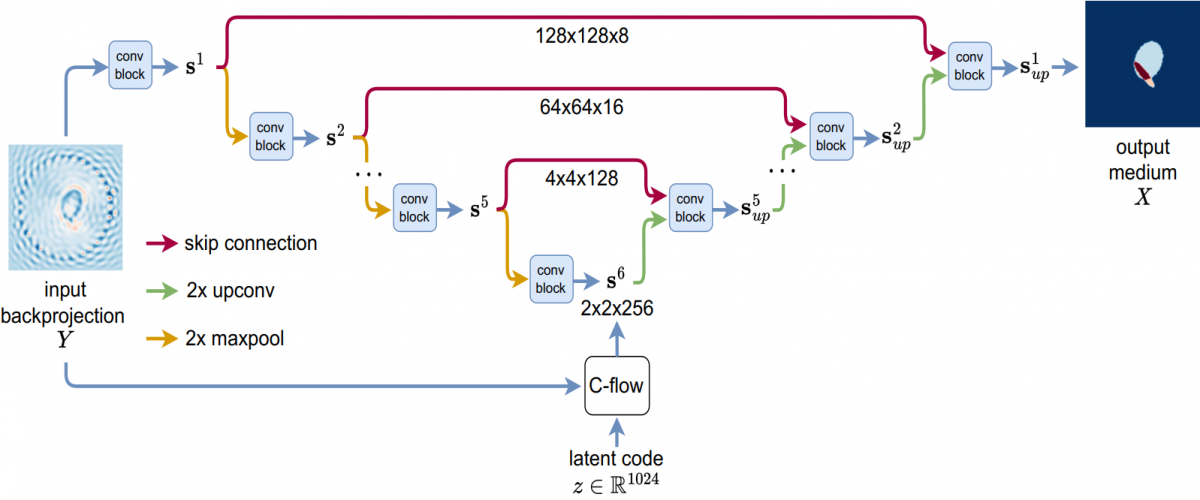
Figure: Network architecture of U-Flow.
Deep Injective Prior for Inverse Scattering
In electromagnetic inverse scattering, we aim to reconsruct object permittivity from scattered waves. Deep learning is a promising alternative to traditional iterative solvers, but it has been used mostly in a supervised framework to regress the permittivity patterns from scattered fields or back-projections. While such methods are fast at test-time and achieve good results for specific data distributions, they are sensitive to the distribution drift of the scattered fields, common in practice. If the distribution of the scattered fields changes due to changes in frequency, the number of transmitters and receivers, or any other real-world factor, an end-to-end neural network must be re-trained or fine-tuned on a new dataset. In this paper, we propose a new data-driven framework for inverse scattering based on deep generative models. We model the target permittivities by a low-dimensional manifold which acts as a regularizer and learned from data. Unlike supervised methods which require both scattered fields and target signals, we only need the target permittivities for training; it can then be used with any experimental setup. We show that the proposed framework significantly outperforms the traditional iterative methods especially for strong scatterers while having comparable reconstruction quality to state-of-the-art deep learning methods like U-Net.
GitHub: https://github.com/swing-research/scattering_injective_prior
Arxiv: https://arxiv.org/abs/2301.03092
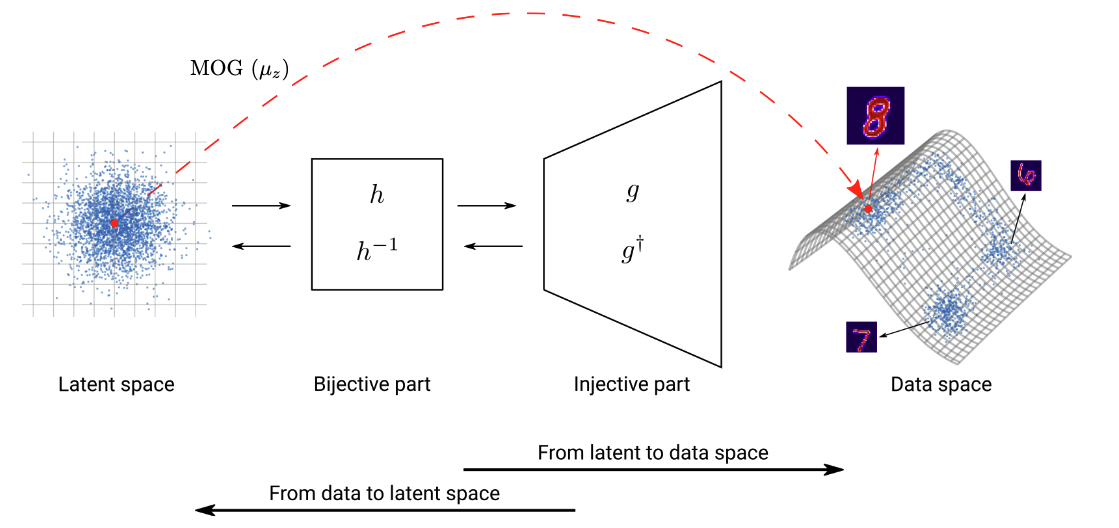
Figure: Injective normalizing flows comprise two submodules, a low-dimensional bijective flow and an injective network with expansive layers.
Publications
2023
@article{ctrumpets,
title={Conditional Injective Flows for Bayesian Imaging},
author={AmirEhsan Khorashadizadeh and Konik Kothari and Leonardo Salsi and Ali Aghababaei Harandi and Maarten de Hoop and Ivan Dokmani\'c},
journal={IEEE Transactions on Computational Imaging},
year={2023},
projectpage = {http://sada.dmi.unibas.ch/en/research/injective-flows},
volume={abs/2204.07664},
eprint={2204.07664},
archivePrefix={arXiv},
url={https://ieeexplore.ieee.org/document/10054422}
}@article{DeepVI,
title={Deep Variational Inverse Scattering},
author={AmirEhsan Khorashadizadeh and Ali Aghababaei and Tin Vlavsi\'c and Hieu Nguyen and Ivan Dokmani\'c},
journal={EUCAP},
year={2023},
projectpage = {http://sada.dmi.unibas.ch/en/research/injective-flows},
volume={abs/2212.04309},
eprint={2212.04309},
archivePrefix={arXiv}
}@article{khorashadizadeh2022deepinjective,
title={Deep Injective Prior for Inverse Scattering},
author={AmirEhsan Khorashadizadeh and Vahid Khorashadizadeh and Sepehr Eskandari and Guy A.E. Vandenbosch and Ivan Dokmani{\'c} },
journal={IEEE Transactions on Antennas and Propagation},
year={2023},
projectpage = {http://sada.dmi.unibas.ch/en/research/injective-flows},
volume={abs/2301.03092},
eprint={2301.03092},
archivePrefix={arXiv}
}2022
@article{puthawala2020globally,
author = {Michael Puthawala and Konik Kothari and Matti Lassas and Ivan Dokmani{\'c} and Maarten de Hoop},
title = {Globally Injective ReLU Networks},
journal = {Journal of Machine Learning Research},
year = {2022},
volume = {23},
number = {105},
pages = {1--55},
url = {http://jmlr.org/papers/v23/21-0282.html}
}2021
@inproceedings{kothari2021trumpets,
title={Trumpets: Injective flows for inference and inverse problems},
projectpage = {http://sada.dmi.unibas.ch/en/research/injective-flows},
author={Kothari, Konik and Khorashadizadeh, AmirEhsan and de Hoop, Maarten and Dokmani{\'c}, Ivan},
booktitle={Uncertainty in Artificial Intelligence},
pages={1269--1278},
year={2021},
organization={PMLR},
url={https://proceedings.mlr.press/v161/kothari21a.html}}